October 22, 1999
How the single
effective rate is calculated
A single effective rate is a constant discount rate that exactly reproduces, except in the instances noted below, the subsidy percentage that was obtained by the “basket-of-zeros” method. The need for a single effective rate arises from the dual requirements of the Federal Credit Reform Act (as amended). First, that the “basket-of-zeros” approach be used for discounting (though it describes that method rather than naming it); and, second, that financing accounts calculate interest earnings on balances deposited with the Treasury or interest payments on borrowings from the Treasury with a rate equivalent to that used for discounting. To meet this dual requirement, the credit subsidy calculator uses the “basket-of-zeros” method to calculate that original subsidy estimate for the budget and, at the same time, a single effective rate, that can be used for all other purposes.
The single effective rate has some characteristics that bear emphasis:
It depends upon the yield curve used to discount and the cash flow observations that are discounted. Thus, for a given set of cash flow observations, the single effective rate obtained for one yield curve will differ from that obtained for another yield curve. Also, for a given yield curve, the single effective rate obtained with one collection of cash flow observations, generally, will differ from that obtained from another collection of cash flow observations. (“Generally,” because there are combinations of changes that would have exactly offsetting effects.)
It is determined by a trial-and-error method, which is described in Appendix A.
It cannot be uniquely determined in all circumstances. Two instances are described below. In the first instance, no single effective rate can be obtained; in the second, the single effective rate is higher than the highest spot rate used to discount the individual cash flow observations.
Finally, instances may arise in which multiple single effective rate exists.
The methods described in this paper (and its appendices) produce a unique single effective rate (if one exists), the most appropriate single effective rate (if more than one exists), or the nearest approximation (if none exists).
Methods, stated
generally
To avoid the problems created by the exceptions noted below, the steps below are followed:
Determine if there is any relationship between the subsidy percentage and the discount rate. If all possible discount rates result in the same subsidy, return a weighted average (defined below) as the single effective rate;
Determine if a single effective rate exists. If not, return a weighted average as the single effective rate;
Determine if there is a unique single effective rate. If so, and if it falls within the bounds of the spot rates used to obtain the basket-of-zeros result, return that value; if not, return the nearest value within the range of values used in the basket-of-zeros computation.
When there are multiple single effective rates and two or more are within the range of values used in the basket-of-zeros computation; return the single effective rate that is closest to the weighted average.
“Weighted average” refers to an average in which (a) spot rates are converted to effective annual yield and (b) are weighted by the absolute values of the cash flow observations, and averaged.
How exceptions
arise
The seemingly anomalous result of not finding a unique, exact single effective rate arises when the relationship between the subsidy and the discount rate is not “monotonic” or not consistently rising or consistently falling in the relevant interval. The following discussion presents three kinds of results from a non-monotonic relationship.
Multiple solutions or no solution can be shown by example. In the following cash flow observations, the important value is the negative value on the third line. The large, negative value reduces the net present value of all cash flows. If the observation on the third line were positive, the relationship between subsidy and discount rate would be monotonic.
|
Observation at the end of year… |
Cash flow observation |
Spot rate (for basket-of-zeros) |
Present value factor |
Present value |
|
1 |
15 |
3.0 |
.97066 |
14.56 |
|
2 |
50 |
4.0 |
.92385 |
46.19 |
|
3 |
-40 |
5.0 |
.86230 |
-34.49 |
|
Total |
25 |
(na) |
(na) |
26.26 |
When we look at the subsidies that result from applying constant alternative discount rates to the cash flow observations above, we find the following:
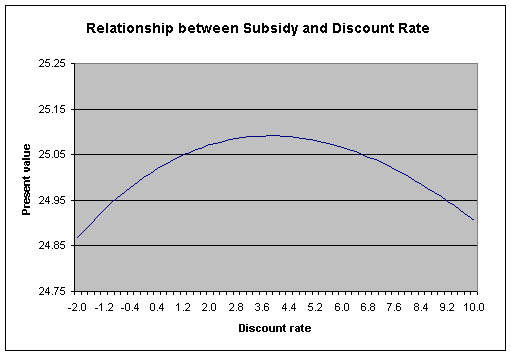
The subsidy reaches a maximum of 25.091 at a constant discount rate of 3.829 percent. It never reaches the target rate of 26.26 percent. Further, had the target subsidy been 25.087, it could have reached this value with a constant discount rate of either 3.00 percent or 4.75 percent.
How common are such patterns of cash flow observations? The parabolic pattern, above, occurs often in practice in loan guarantee programs, though not to the severe degree shown in the chart above. In many loan guarantee programs, there is a delicate balance among the positive values in the near term (upfront fees and annual fees) and negative values in the middle term (payments on defaults) and positive values again in the long term (recoveries on defaults). Of course, the mere presence of positive and negative values does not guarantee a parabola in the relevant range of values. A parabolic pattern, such as the one shown above, results when positive and negative values are concentrated in certain time periods and have substantially offsetting contributions on the net present value result.
A single effective rate outside the expected range can also occur. On the surface, one might reasonably expect that the single effective rate would lie somewhere in the interval from the lowest spot rate to the highest spot rate used in the basket-of-zeros approach. But that does not always happen. Here’s an example:
|
Observation at the end of year… |
Cash flow observation |
Spot rate (for basket-of-zeros) |
Present value factor |
Present value |
|
0 |
10.000 |
3.00 |
1.00000 |
10.0000 |
|
1 |
-10.404 |
4.00 |
0.96117 |
-10.0000 |
|
Total |
|
|
|
0.0000 |
Obviously, because only one observation is affected by the discount rate, the single effective rate to obtain a subsidy of exactly zero is 4.00 percent (after conversion to an effective annual yield). Now, consider a trivial modification of this example:
|
Observation at the end of year… |
Cash flow observation |
Spot rate (for basket-of-zeros) |
Present value factor |
Present value |
|
0.04* |
10.000 |
3.00 |
0.99876 |
9.9876 |
|
1 |
-10.404 |
4.00 |
0.96117 |
-10.0000 |
|
Total |
|
|
|
-0.0124 |
* 1/24th or approximately 0.04 corresponds to a cash flow observation occurring two weeks after the start of the fiscal year.
Now, the single effective rate increases to approximately 4.08, which is higher than the rate used for any observation.
Note about the appendices
Appendix A give a more complete description of the numerical methods used to evaluate whether intervals are monotonic and find solutions with reasonable efficiency.
Appendix B gives some references to published works that provide more details on numerical methods, including some the methods described in Appendix A.
Appendix A: Numerical methods
used to compute the single effective rate
The method used to find the single effective rate is a variant of the “interval bisection” approach, described in several published sources on numerical methods, some of which are listed at the end of this paper.
Definitions:
RL, RU Interest rates at the lower and upper bounds of the search interval.
The lower bound is -199 percent. At -200 percent, the expression 1 + r/200 becomes zero. Raised to any power it would still be zero and unsuitable as a denominator. Values lower than -200 percent would result in imaginary roots. (Technically, there are mathematically valid values between -199 and -200; however, these are treated as out-of-range values.)
The upper bound is approximately 10308 percent, which is the largest value that can be represented in computer memory for the number format used in the CSC (8-byte floating point value or “double”).
Rl, Rm, Ru Interest rates at the lower bound, mid-point, and upper bound of the subset of the interval being tested in a particular iteration.
sub (r) A function that returns the subsidy percentage computed for a given set of cash flows and an interest rate r. (Described in How the subsidy and its components are derived from cash flow observations.)
mid (r1, r2) A function that returns the mid-point between interest rates r1 and r2, computed as the arithmetic mean of the two values when they are of the same order of magnitude and the geometric mean when the orders of magnitude differ.
monotonic (r1, r2) A function that returns “true” when the subsidies calculated in the interval from r1 and r2 are monotonically increasing or decreasing and “false” otherwise. (Methods are described below.)
has (r1, r2) A function that returns “true” when the target subsidy lies between the sub (r1) and sub (r2) and “false” otherwise. Obviously, for this to work reliably, the expression monotonic (r1, r2) must be “true.” (Methods are described below.)
find (r1, r2) A function that returns the value of r for which sub (r) exactly matches the target subsidy value. This expression is undefined for intervals in which the expression has (r1, r2) is “false.” (Methods are described below.)
avg() A function that returns the average spot rate, converted to an effective annual yield, that is weighted by the cash flow observations, without regard to sign.
General method:
Evaluate sub (r) at five values of r, equally spaced in the interval of spot rates used for calculating the subsidy. If successive values of sub (r), proceeding from the lowest to the highest value of r, are within 0.0001 of each other, then the subsidy may be considered to be insensitive to the discount rate assumptions. In such cases, return avg( ).
Set Rl to RL, Ru to RU, and Rm to mid (Rl, Ru).
If the expression monotonic (rl, ru) and has (rl, ru) are “true,” evaluate find (rl, ru) to obtain the single effective rate. If the result of find (rl, ru) is within the interval of spot rates used for calculating the subsidy, return it; otherwise, take the nearest spot rate used in calculating the subsidy, convert it to an effective annual yield, and return that value.
If the expression monotonic (rl, ru) is “true” and has (rl, ru) is “false,” return avg ( ) and issue a warning message that the exact single effective rate could not be found.
If the expression monotonic (rl, ru) is “false,” repetitively divide the interval in half until all subintervals are monotonic, then evaluate has (r1, r2) for each subinterval, and evaluate find (r1, r2) where has (r1, r2) is “true.” If more than one solution is found, return the solution closest to avg ( ).
If the preceding step fails to find a result, return avg ( ).
In any instance where intervals are subdivided, the minimum interval is 0.02 basis points. When intervals are smaller than that, it becomes increasingly difficult (because of limitations in computer arithmetic) to find meaningful first derivatives.
Method for monotonic (r1, r2)
This expression evaluates to “true” when each successive value of sub (r), calculated from r1 to r2, is consistently equal to or greater than the previous value or is consistently equal to or less than the previous value.
There is no convenient way to directly determine if the values of sub (r1) through sub (r2) are monotonic. First, these subsidy values are derived from a collection of cash flow observations, which will vary widely in number and need not follow any pattern of regularity. The values of sub (r1) through sub (r2) would follow a polynomial of a fairly high order with a trivially less complex first derivative. Second, because there is an infinite number (or, in computer representations, a very large, but finite number) of such observations, direct evaluation of all possible points is impractical.
The method used is an approximation in which the first derivative is estimated at the beginning and end of the interval and at three equally spaced points within the interval. If these estimated derivatives all have the same sign and if each successive derivative is either equal to or greater than the previous or is equal to or less than the previous, the values in the interval are assumed to be monotonic.
Though more strict than the actual definition of “monotonic,” this working definition can be easily and efficiently computed.
Apart from that limitation, this method should work in this context because the values being tested are subsidy percentages that are derived from a monotonically varying discount rate and a given set of cash flow observations that do not change as the discount rate changes. The cash flow observations tend to be numerous, generally in the hundreds, and the subsidy percentage is a polynomial function in the form:
sub (r) = b1 + b2xn + b3xn + …
where the bn are the cash flow observations and the xn are discount factors with a suitable exponent. Consequently, the function will be continuous and often of a fairly high order, which will tend to neutralize the shortcomings of the method.
Method for has (r1, r2)
Return “true” if the target value for the subsidy lies in the interval sub (r1) and sub (r2) and “false” otherwise. The returned value is guaranteed to be accurate only when monotonic (r1, r2) is “true.”
The return value is determined from sub (r1) and sub (r2) by the following:
If sub (r1) is less than or equal to the target: return “true” when sub (r2) is equal to or greater than the target and “false” otherwise.
If sub (r1) is equal to or greater than the target: return “true” when sub (r2) is less than or equal to the target and “false” otherwise.
Method for find (r1, r2)
Return the discount rate that exactly produces the target subsidy percentage. It is undefined in intervals where has (r1, r2) is “false.” The function uses a variant of the “interval bisection” method. Specifically:
Initial steps: Set Rl to r1
and Ru to r2.
Iteration: Set Rm to mid (Rl, Ru).
If the difference between Rm and Ru is negligible, use Rm as the result of the evaluation of the function and cease iteration.
If the target subsidy percentage lies between sub(Rl) and sub(Rm), set Ru to Rm; otherwise, set Rl to Rm and iterate again.
Appendix B: References
Steven C. Charpa and Raymond P. Canale, Numerical Methods for Engineers, Third Edition (New York: WCB/McGraw-Hill, 1998).
Gisela Engeln-Mullges and Frank Uhlig, Numerical Algorithms with C (New York: Springer-Verlag, 1996).
B. H. Flowers, An Introduction to Numerical Methods in C++ (Oxford: Oxford University Press, 1995).
Thomas A. Grandine, The Numerical Methods Programming Projects Book (Oxford: Oxford University Press, 1990).
John H. Mathews, Numerical Methods (Englewood Cliffs, NJ: Prentice-Hall, 1992).
William H. Press, Saul A. Tenkolsky, William T. Vetterling, and Brian P. Flannery, Numerical Recipes in C, Second Edition (Cambridge: Cambridge University Press, 1992).
John R. Rice, Numerical Methods, Software, and Analysis (Boston: Academic Press, 1992).
Sidney Yakowitz and Ferene Szidarorszky, An Introduction to Numerical Computation (New York: MacMillan, 1989).
